Reinforcement Learning
- Introduction
- What is reinforcement learning ?
- State Monad
- State of the board
- Haskell Gloss
- Value table
- How do we know that a Player has won ?
- The representation of a Player
- Calculate the next state in the board.
- Greedy move
- Abandoning the functional approach with this function
- Equivalent of ‘run’ function in the example
- Equivalent of ‘runs’ function in the example
- Main function
- Number of times Player O wins over X
Introduction
I am going through Reinforcement Learning: An Introduction by Richard S. Sutton and Andrew G. Barto and porting the lisp examples to Haskell in order to learn RL mainly but also to hone my functional programming skills. I chose the lisp examples over C examples obviously because I am coding Haskell. Not that lisp and Haskell are similar. Far from it. They are dissimilar but I find that it is helpful to work off a language that is not procedural.
The lisp code for this example I referred to is this
Except the Haskell code everything I explain is based on the references cited at the end.
What is reinforcement learning ?

State Monad
I started with a proper Haskell state management workflow but soon abandoned it in favour of mutable IOarrays. Global mutable state is virtually non-existent in Haskell code.
This code just manages the board size but is unused now. The board is small and is of fixed size.
fun :: Map.Map String Int
fun = Map.empty
store :: String -> Int-> State (Map.Map String Int) ()
store x value = do
fun <- get
put (Map.insert x value fun)
retrieve :: String -> State (Map.Map String Int) (Maybe (Int))
retrieve roworcolumn = do
fun <- get
return (Map.lookup roworcolumn fun)
getrow = do {store "row" 1; retrieve "row"}
getcolumn = do {store "column" 1; retrieve "column"}
getboardsize = do
let x = (runState getrow fun) in
let y = (runState getcolumn fun) in
(Just (*) <*> (fst x) <*> (fst y) )State of the board
data BoardState = BoardState { xloc :: [Int],
oloc :: [Int],
index :: Int
} deriving (Show)Haskell Gloss
The UI toolkit Gloss was used to initially display a grid. I hoped that eventually I could debug this visually. That hope turned out to be false as I misjudged the number of times one trains an algorithm like this. So this code is not useful for debugging.
translationaccumulator :: [Int] -> [Int] -> [(Float,Float)] -> [Picture] -> [Picture]
translationaccumulator [] _ _ ys = reverse ys
translationaccumulator _ [] _ ys = reverse ys
translationaccumulator (head1:xs1) (head:xs) angle ys = let (a,b) = (angle !!(head - 1)) in
let (c,d) = (angle !!(head1 - 1)) in
translationaccumulator xs1 xs angle ( ((translate a b) $
drawx ) : ((translate c d) $
drawo ):ys)
drawBoard :: BoardState -> Picture
drawBoard (BoardState xloc oloc index)=
Pictures $ [ translate x y $ rectangleWire 90 90| x<-[0,90..180], y<-[0,90..180] ] ++ (translationaccumulator xloc oloc [(0,180),(90,180),(180,180),(0,90),(90,90),(180,90),(0,0),(90,0),(180,0)] [])
drawx :: Picture
drawx = color green $ rotate 45 $
pictures [rectangleWire 1 45, rectangleWire 45 1]
drawo :: Picture
drawo = color rose $ thickCircle 25 2Value table
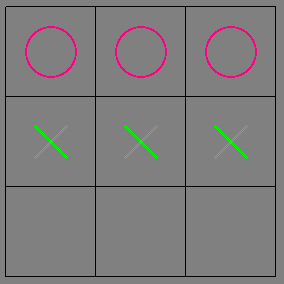
The representation of the board state when Player X has moved to position 1 and Player O has learned to move to position 1 is [1] and [1]. This means that the two lists, representing the positions played by the two players X and O, each contain 1
This is stored as a set of higher-order bits and a set of lower-order bits like this in the value table. The value of this set of bits shown in the image is 513.

stateindex :: [Int] -> [Int] -> Int
stateindex xloc oloc = sum [2^(n-1)| n <- xloc]
+ 512 * sum [2^(n-1) | n <- oloc]How do we know that a Player has won ?
Just store all the winning combinations and check because we have less board positions.
winningcombination :: [[Int]]
winningcombination = [[1,2,3],[4,5,6],[7,8,9],
[1,4,7],[2,5,8],[3,6,9],
[1,5,9],[3,5,8]]
checkallcombination :: [Int] -> Bool
checkallcombination l = let wc = winningcombination in
loop wc
where
loop :: [[Int]] -> Bool
loop wc =
case wc of
[] -> False
(x:xs) -> if containscombination x l then True else loop xs
containscombination :: [Int] -> [Int] -> Bool
containscombination xs xs1 =
case xs of
[] -> True
(x:xss) -> if (x `elem` xs1) then containscombination xss xs1 else FalseThe ReaderT Monad transformer for reading and writing to arrays.
createarray :: IO ( IOArray Int Double)
createarray = do {
arr <- newArray (0,512*512) (-1.0);
return arr
}
type ArrayAccess = ReaderT (IOArray Int Double) IO
type ArrayWriteAccess = ReaderT (IOArray Int Double) IO()
readvalue :: Int -> ArrayAccess Double
readvalue x = do
a <- ask
b <- liftIO( readArray a x);
return b
writevalue :: Int -> Double -> ArrayWriteAccess
writevalue x y = do
a <- ask
liftIO( writeArray a x y)
-- Test array accesses
readfromarray = do { a <- createarray; liftIO (runReaderT (readvalue 1) a) }
writetoarray = do { a <- createarray; liftIO (runReaderT (writevalue 1 2) a) }The representation of a Player
data Player = X | O deriving Show
isX :: Player -> Bool
isX X = True
isX O = False Calculate the next state in the board.
Get a list of empty positions in the board.
-- Returns a list of unplayed locations
possiblemoves :: BoardState -> [Int]
possiblemoves (BoardState xloc oloc index) =
let xs = [1,2,3,4,5,6,7,8,9] in
(xs \\ xloc) \\ oloc```
Select an empty position randomly
-- "Returns one of the unplayed locations, selected at random"
randommove :: BoardState -> IO Int
randommove state =
let possibles = possiblemoves state in
case possibles of
p -> fmap (p !! ) $ randomRIO(0, length p - 1)Greedy move
greedymove :: (String -> IO()) ->( IOArray Int Double) ->Player -> BoardState -> IO (Int,IOArray Int Double)
greedymove log a player state =
let possibles = possiblemoves state in
case possibles of
[] -> return (0, a)
p -> let bestvalue = -1.0 in-- Since default value in array is -1.0
let bestmove = (head p) in
choosebestmove a p bestvalue bestmove
where
choosebestmove arr [] bestvalue1 bestmove1 = return (0,a)
choosebestmove arr (x:xs) bestvalue1 bestmove1 = do
(nv,b) <- nextvalue logs player x arr state
xvalue <- catch (readthevalue b (ReinforcementLearning.index (nv)))(\(SomeException e) -> printf "Reading [%d} in greedy move" x >> print e >> throwIO e)
case compare bestvalue1 xvalue of
LT -> choosebestmove b xs xvalue x;
GT -> return (bestmove1,b)
EQ -> return (bestmove1,b)
Abandoning the functional approach with this function
This is basically the original Lisp converted line by line to Haskell. The Haskell programmers who I consulted dissuaded me from doing this but at this time my Haskell knowledge does not measure up to the task.
gameplanrevised :: (String -> IO()) ->( IOArray Int Double) -> BoardState -> BoardState -> IO (IOArray Int Double,BoardState,Double)
gameplanrevised log a state newstate = do
exploremove a state newstate
where
exploremove :: ( IOArray Int Double) -> BoardState -> BoardState ->IO (IOArray Int Double,BoardState,Double)
exploremove a state newstate =
do
r <- randombetween;
let em = exploratorymove r in
do
result <- (terminalstatep log a (ReinforcementLearning.index newstate));
case result of
True -> do
b <- update a state newstate
valueofnewstate <- catch (readthevalue b (ReinforcementLearning.index newstate)) (\(SomeException e) -> print e >> mapM_ (putStr . show) [ (ReinforcementLearning.index newstate)]>> throwIO e)
return (b,newstate,valueofnewstate)
False -> do
if em
then do
rm <- randommove newstate
(nv,d) <- nextvalue logs O rm a newstate
result1 <- (terminalstatep log d (ReinforcementLearning.index nv));
valueafterrandommove <- catch (readthevalue d (ReinforcementLearning.index nv)) (\(SomeException e) -> print e >> mapM_ (putStr . show) [ (ReinforcementLearning.index nv)]>> throwIO e)
if result1
then do
return (d,nv,valueafterrandommove)
else do
r1 <- randommove nv
(ns,na) <- nextvalue logs X r1 d nv
exploremove na nv ns
else do
(gm,c) <- greedymove log a O newstate
(nv',d') <- nextvalue logs O gm c newstate
d'' <- update d' state nv'
result2 <- (terminalstatep log d'' (ReinforcementLearning.index nv'));
valueaftergreedymove <- catch (readthevalue d'' (ReinforcementLearning.index nv')) (\(SomeException e) -> print e >> mapM_ (putStr . show) [ (ReinforcementLearning.index nv')]>> throwIO e)
if result2
then do
return (d'',nv',valueaftergreedymove)
else do
r1 <- randommove nv'
(ns,na) <- nextvalue logs X r1 d'' nv'
exploremove na nv' ns Equivalent of ‘run’ function in the example
playntimes :: IOArray Int Double -> (String -> IO()) ->Int -> IO (IOArray Int Double,Double)
-- playntimes log n = do a <- createarray;
playntimes a log n = do writethevalue a 0 0.5
r <- (randommove (BoardState [] [] 0))
playtime (BoardState [] [] 0) (nextvalue logs X r a (BoardState [] [] 0)) n 0 r
where
playtime :: BoardState -> IO (BoardState,IOArray Int Double) -> Int -> Double -> Int -> IO (IOArray Int Double,Double)
playtime s ns n acc r --finala is the consolidation for the next run
| n == 0 = do logsresult $ printf "Played 100 times %f %f" acc (acc/100.0)
(_, b) <- ns
return (b,acc)
| n > 0 = do
(boardstate, b) <- ns
(updatedarray, _, result) <- game logs s boardstate b;
r1 <- randommove (BoardState [] [] 0)
playtime (BoardState [] [] 0) (nextvalue logs X r1 updatedarray (BoardState [] [] 0)) (n - 1) (acc + result) r1
Equivalent of ‘runs’ function in the example
numruns :: IOArray Int Double ->Int -> Int -> Int -> Int -> IO()
numruns arr n1 n bins binsize
| n == 0 = printf "\nPlayed numruns times"
| n > 0 = do
p <- createarray
writethevalue p 0 0.5
b <- playrepeatedly p arr n1 bins binsize
numruns arr n1 (n -1) bins binsize
playrepeatedly :: IOArray Int Double ->IOArray Int Double -> Int -> Int -> Int -> IO(IOArray Int Double)
playrepeatedly a arr numrun1 numbins binsize = do
loop a 0 binsize
where
loop a i bs
| i == numbins = let x = numrun1
y = numbins
z = binsize in
loop1 a x 0 y z
| i < numbins = do
(b,acc) <- playntimes a logs bs;
lastvalue <- readthevalue arr i
writethevalue arr i (lastvalue + acc)
loop b (i+1) bs
where
loop1 a x j y z = if j < y
then do
fv <- readthevalue arr j
printf " Runs %f Final Value %f Binsize %d Numruns %d \n" (fv / fromIntegral( z * x)) fv z x
loop1 a x (j+1) y z
else
return aMain function
main = let numbins = 30 in
do
arr <- newArray (0,numbins) 0.0;
ReinforcementLearning.numruns arr 1 1 numbins 100 -- numruns numruns numbins binsize
return ()Number of times Player O wins over X
The Reinforcement Learning agent should become unbeatable. That is what I used to think. But my code makes Player O learn and win roughly more than 50 % but less than or equal to 60%. But I have only played 100 games, 30 times each.
I think the winning rate of Player O should be more. It is less because somewhere in my code there may be a bug. I will continue to test it and the latest code will be in my repository
"Played 100 times 45.0 0.45"
"Played 100 times 53.0 0.53"
"Played 100 times 51.0 0.51"
"Played 100 times 52.0 0.52"
"Played 100 times 44.0 0.44"
"Played 100 times 46.0 0.46"
"Played 100 times 52.0 0.52"
"Played 100 times 51.0 0.51"
"Played 100 times 38.0 0.38"
"Played 100 times 39.0 0.39"
"Played 100 times 39.0 0.39"
"Played 100 times 43.0 0.43"
"Played 100 times 48.0 0.48"
"Played 100 times 49.0 0.49"
"Played 100 times 52.0 0.52"
"Played 100 times 56.0 0.56"
"Played 100 times 50.0 0.5"
"Played 100 times 43.0 0.43"
"Played 100 times 50.0 0.5"
"Played 100 times 51.0 0.51"
"Played 100 times 64.0 0.64"
"Played 100 times 50.0 0.5"
"Played 100 times 61.0 0.61"
"Played 100 times 58.0 0.58"
"Played 100 times 46.0 0.46"
"Played 100 times 60.0 0.6"
"Played 100 times 55.0 0.55"
"Played 100 times 51.0 0.51"
"Played 100 times 51.0 0.51"
"Played 100 times 56.0 0.56"
References
- https://mitpress.mit.edu/books/reinforcement-learning
- The code from 1998 when the book was published is http://incompleteideas.net/sutton/book/code/TTT.lisp