Toy Generatively Pretrained Transformer (GPT)
- tl;dr
- Stage 1
- Matrix multiplication trick using triangular matrix
- Self-attention
- Further architectural changes
- Conclusion
Yet another attempt to closely replicate the popular PyTorch code of https://karpathy.ai/zero-to-hero.html close on the heels of the exploration of basic https://mohanr.github.io/Exploring-Transformer-Architecture/.
I have ported the code to TensorFlow and may have caused a bug or two which are not evident. But the code works as I expected. But this is just the beginning stage. At this point there is no GPT.
tl;dr
- The flow of the article mirrors the way the code is developed iteratively
- I haven’t coded this to use batches at this time hoping to add it later. Nor have I split the dataset to get a validation set.
- In many cases I had to execute the PyTorch code to understand the shapes. Yet some shape here or there may be wrong but the code executes without errors.
- The final code is here and further improvements will be committed.
- I haven’t specifically trained using a GPU but with some some simple code changes it can be.
Stage 1
The dataset used here is not cleaned. There are characters and numbers in it. So newlines are removed but data can be properly fed at a later stage.
import tensorflow as tf
import tensorflow_probability as tfp
from keras.layers import Embedding
input = tf.io.read_file("/Users/anu/PycharmProjects/TensorFlow2/shakespeare.txt")
input = tf.strings.strip(input)
input = tf.strings.regex_replace(input,' +', '')
input = tf.strings.regex_replace(input,'\n', '')
length = int(tf.strings.length(input))
vocab = tf.strings.unicode_split_with_offsets(input, 'UTF-8')
elem,idx = tf.unique(vocab[0])
vocab_size = len(elem)
print(f'Size of vocabulary={vocab_size}')
table = tf.lookup.StaticHashTable(
initializer=tf.lookup.KeyValueTensorInitializer(
keys=elem,
values=tf.constant([idx for idx, inp in enumerate(elem)]),
),
default_value=tf.constant(-1),
name="elemtoindex"
)
indextoelem = tf.lookup.StaticHashTable(
initializer=tf.lookup.KeyValueTensorInitializer(
keys=tf.strings.as_string([idx for idx, inp in enumerate(elem)]),
values=elem,
),
default_value=tf.constant('-1'),
name="indextoelem"
)
def random_sample(text):
rand = tf.random.uniform(shape=[], minval=1, maxval=length - 201)
start = int(rand)
# print(f'Start={int(rand)} Length={length} End={start + 200 + 1}')
return tf.strings.substr(text,start, 201, unit='BYTE')
global samplelist,reversesamplelist
samplelist = []
reversesamplelist = []
def reverse_map_fn(bytes):
reversesamplelist.append(indextoelem.lookup(tf.strings.as_string(bytes)))
return bytes
def map_fn(bytes):
samplelist.append(table.lookup(bytes))
return bytes
def draw_random_sample(block_size):
sample = tf.strings.substr(input,0, block_size, unit='BYTE')
split_sample = tf.strings.bytes_split(sample)
tf.map_fn(map_fn, tf.strings.bytes_split(split_sample))
global samplelist
reverse_map(samplelist[:-1])
X,y = (tf.stack(samplelist[:-1]),tf.stack(samplelist[1:]))
samplelist = []
return X,y
def reverse_map(X):
tf.map_fn(reverse_map_fn, X)
X,y = draw_random_sample(9)
print(reversesamplelist)
vocab_size = len(elem)
def decode(idx):
return idx,indextoelem.lookup(
tf.strings.as_string([inp for inp, inp in enumerate(idx)]))The model sub-class is simple and accepts the entire sequence of characters everytime. But we are predicting the next character only based on the previous character. This will be addressed later.
tf.Tensor([0], shape=(1,), dtype=int64)
tf.Tensor([0 8], shape=(2,), dtype=int64)
tf.Tensor([ 0 8 43], shape=(3,), dtype=int64)
tf.Tensor([ 0 8 43 67], shape=(4,), dtype=int64)
tf.Tensor([ 0 8 43 67 5], shape=(5,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31], shape=(6,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31], shape=(7,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21], shape=(8,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51], shape=(9,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23], shape=(10,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23 2], shape=(11,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23 2 2], shape=(12,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23 2 2 56], shape=(13,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23 2 2 56 1], shape=(14,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23 2 2 56 1 55], shape=(15,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23 2 2 56 1 55 36], shape=(16,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23 2 2 56 1 55 36 12], shape=(17,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23 2 2 56 1 55 36 12 27], shape=(18,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23 2 2 56 1 55 36 12 27 31], shape=(19,), dtype=int64)
tf.Tensor([ 0 8 43 67 5 31 31 21 51 23 2 2 56 1 55 36 12 27 31 38], shape=(20,), dtype=int64)The is the TensorFlow code that should produce the same result as the original PyTorch code. The loop structures are all different though.
class BigramModel(tf.keras.Model):
def __init__(self,vocab_size):
super().__init__()
self.token_embedding_table = Embedding(vocab_size,vocab_size)
def call(self,idx,targets=None):
logits=self.token_embedding_table(idx)
if targets is None:
loss = None
else:
bce = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
loss = bce(targets,tf.squeeze(logits)).numpy()
return logits, loss
def generate(self,idx,max_new_tokens):
i = tf.constant(0)
c = lambda i, d: tf.less(i, max_new_tokens)
def b(i, idx):
logits,loss = self(idx)
logits = logits[-1]
# print(f'Shape of logits is {tf.shape(logits)}')
probs = tf.nn.softmax(logits)
# print(f'Shape of probs is {tf.shape(probs)}')
idx_next = tfp.distributions.Multinomial(total_count=1,probs=probs)
# print(f'Shape of sample is {tf.shape(idx_next.sample(1))}')
idx = tf.concat([idx,
tf.reshape(tf.squeeze(
tf.cast(tf.where(
tf.reshape(idx_next.sample(1),(vocab_size))),tf.int64))
,(1,))],0)
return tf.add(i, 1), idx
_, idx1 = tf.while_loop(c, b, loop_vars=[i, idx])
return idx1Last time step
Only the last dimension in this output is considered for predictng the next one character at this time.
So in this example the last dimension is highlighted.
x = tf.random.uniform((4,4))
print(x)
print(x[-1])tf.Tensor(
[[0.6044643 0.9598156 0.84220576 0.6529906 ]
[0.03485656 0.1756084 0.9860773 0.8582853 ]
[0.45344257 0.6370505 0.9529482 0.4074465 ]
[0.27584124 0.44224763 0.7260096 0.16439259]], shape=(4, 4), dtype=float32)

Generation
This generates these 20 characters.
m = BigramModel(len(elem))
out,loss = m(tf.reshape(X,(1,8)),tf.reshape(y,(1,8)))
idx, generation = decode(m.generate(tf.zeros((1,),tf.int64),20))
print(["".join(i) for i in generation.numpy()[:].astype(str)])[‘1’, ‘T’, ‘0’, ‘V’, ‘S’, ‘.’, “’”, ‘.’, ‘n’, ‘U’, ‘t’, ‘8’, ‘l’, ‘M’, “’”, ‘T’, ‘g’, ‘b’, ‘N’, ‘i’, ‘h’]
Training Stage 1
This is the entire code again as small changes have been made to train.
import tensorflow as tf
import tensorflow_probability as tfp
from keras.layers import Embedding
input = tf.io.read_file("/Users/anu/PycharmProjects/TensorFlow2/shakespeare.txt")
input = tf.strings.strip(input)
input = tf.strings.regex_replace(input,' +', '')
input = tf.strings.regex_replace(input,'\n', '')
length = int(tf.strings.length(input))
vocab = tf.strings.unicode_split_with_offsets(input, 'UTF-8')
elem,idx = tf.unique(vocab[0])
vocab_size = len(elem)
print(f'Size of vocabulary={vocab_size}')
block_size = 9
table = tf.lookup.StaticHashTable(
initializer=tf.lookup.KeyValueTensorInitializer(
keys=elem,
values=tf.constant([idx for idx, inp in enumerate(elem)]),
),
default_value=tf.constant(-1),
name="elemtoindex"
)
indextoelem = tf.lookup.StaticHashTable(
initializer=tf.lookup.KeyValueTensorInitializer(
keys=tf.strings.as_string([idx for idx, inp in enumerate(elem)]),
values=elem,
),
default_value=tf.constant('-1'),
name="indextoelem"
)
def random_sample(text):
rand = tf.random.uniform(shape=[], minval=1, maxval=length - 201)
start = int(rand)
# print(f'Start={int(rand)} Length={length} End={start + 200 + 1}')
return tf.strings.substr(text,start, 201, unit='BYTE')
global samplelist,reversesamplelist
samplelist = []
reversesamplelist = []
def reverse_map_fn(bytes):
reversesamplelist.append(indextoelem.lookup(tf.strings.as_string(bytes)))
return bytes
def map_fn(bytes):
samplelist.append(table.lookup(bytes))
return bytes
def random_sample(text,block_size):
rand = tf.random.uniform(shape=[], minval=1, maxval=length - (block_size + 1))
start = int(rand)
# print(f'Start={int(rand)} Length={length} End={start + block_size + 1}')
return tf.strings.substr(text,start, block_size, unit='BYTE')
def draw_random_sample(block_size):
sample = random_sample(input,block_size)
split_sample = tf.strings.bytes_split(sample)
tf.map_fn(map_fn, tf.strings.bytes_split(split_sample))
global samplelist
reverse_map(samplelist[:-1])
X,y = (tf.stack(samplelist[:-1]),tf.stack(samplelist[1:]))
samplelist = []
return X,y
def reverse_map(X):
tf.map_fn(reverse_map_fn, X)
X,y = draw_random_sample(block_size)
print(reversesamplelist)
vocab_size = len(elem)
def decode(idx):
return idx,indextoelem.lookup(
tf.strings.as_string([inp for inp, inp in enumerate(idx)]))
class BigramModel(tf.keras.Model):
def __init__(self,vocab_size):
super().__init__()
self.token_embedding_table = Embedding(vocab_size,vocab_size)
def call(self,idx,targets=None):
logits=self.token_embedding_table(idx)
if targets is None:
loss = None
else:
bce = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
# loss = bce(targets,tf.squeeze(logits)).numpy()
loss = bce(targets, tf.squeeze(logits))
return logits, loss
def generate(self,idx,max_new_tokens):
i = tf.constant(0)
c = lambda i, d: tf.less(i, max_new_tokens)
def b(i, idx):
logits,loss = self(idx)
logits = logits[-1]
# print(f'Shape of logits is {tf.shape(logits)}')
probs = tf.nn.softmax(logits)
# print(f'Shape of probs is {tf.shape(probs)}')
idx_next = tfp.distributions.Multinomial(total_count=1,probs=probs)
# print(f'Shape of sample is {tf.shape(idx_next.sample(1))}')
idx = tf.concat([idx,
tf.reshape(tf.squeeze(
tf.cast(tf.where(
tf.reshape(idx_next.sample(1),(vocab_size))),tf.int64))
,(1,))],0)
return tf.add(i, 1), idx
_, idx1 = tf.while_loop(c, b, loop_vars=[i, idx])
return idx1
m = BigramModel(len(elem))
out,loss = m(tf.reshape(X,(1,block_size -1)),tf.reshape(y,(1,block_size-1)))
idx, generation = decode(m.generate(tf.zeros((1,),tf.int64),20))
print(["".join(i) for i in generation.numpy()[:].astype(str)])
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
epochs = 2
for epoch in range(epochs):
print("\nStart of epoch %d" % (epoch,))
for step in range(20000):
with tf.GradientTape() as tape:
x,y = draw_random_sample(block_size)
logits,loss = m(tf.reshape(x, (1, block_size - 1)), tf.reshape(y, (1, block_size - 1)))
grads = tape.gradient(loss, m.trainable_weights)
# Run one step of gradient descent by updating
# the value of the variables to minimize the loss.
optimizer.apply_gradients(zip(grads, m.trainable_weights))
# Log every 200 batches.
if step % 200 == 0:
print(
"Training loss at step %d: %.4f"
% (step, float(loss))
)
print("Seen so far: %s samples" % ((step + 1)))
_, generation = decode(m.generate(tf.zeros((1,),tf.int64),20))
print(["".join(i) for i in generation.numpy()[:].astype(str)])Matrix multiplication trick using triangular matrix
I am reusing this code I contributed to Stackoverflow years back with appropriate changes introduced by TensorFlow 2 API. This code can be refactored and improved but at this time it works.
What does the resulting matrix look like ? The logic if the code now creates a lower triangular matrix( or upper triangular matrix, if we want it) like this.
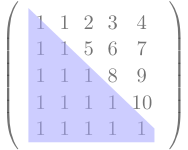
x = tf.constant(tf.ones(10,))
ones = tf.ones((5,5),dtype=tf.int64) #size of the output matrix
mask_a = tf.linalg.band_part(ones, -1, 0) # Upper triangular matrix of 0s and 1s
mask_b = tf.linalg.band_part(ones, 0, 0) # Diagonal matrix of 0s and 1s
mask = tf.subtract(mask_a, mask_b) # Mask of upper triangle above diagonal
zero = tf.constant(0, dtype=tf.int64)
non_zero = tf.not_equal(mask, zero) #Conversion of mask to Boolean matrix
indices = tf.where(non_zero) # Extracting the indices of upper trainagle elements
out = tf.SparseTensor(indices,x,dense_shape=tf.cast((5,5),dtype=tf.int64))
dense = tf.slice(tf.sparse.to_dense(out), [1, 0], [3, 3])
tf.print(dense)
dense = dense / tf.reduce_sum(dense,1,keepdims=True)
print(dense)
random_ints = tf.random.uniform(shape=(3,2), minval=1., maxval=5.)
print(random_ints)
print(tf.matmul(dense,random_ints))The output is this.
[[1 0 0]
[1 1 0]
[1 1 1]]
tf.Tensor(
[[1. 0. 0. ]
[0.5 0.5 0. ]
[0.33333334 0.33333334 0.33333334]], shape=(3, 3), dtype=float32)
tf.Tensor(
[[2.1591725 2.7532902]
[3.748231 4.6269817]
[2.0407896 2.2444978]], shape=(3, 2), dtype=float32)
tf.Tensor(
[[2.1591725 2.7532902]
[2.9537017 3.690136 ]
[2.6493979 3.2082565]], shape=(3, 2), dtype=float32)The trick give us a matrix that has rows based on weighted averages like this.

Self-attention
Explanation will be added in due course as this code implements the first view of self-attention. This is the test code executed separately.
Please note that the elaborate example shown above can be shortened for our purposes to
wei = tf.linalg.band_part(wei, -1, 0)Test code is this.
head_size = 16
tf.random.set_seed(3227)
head_size = 16
B,T,C = 1,8,32 # batch, time, channels
x = tf.random.normal((B,T,C))
key = tf.keras.layers.Dense( head_size, input_shape=(32,), activation=None,use_bias=False)
query = tf.keras.layers.Dense(head_size,input_shape=(32,),activation=None,use_bias=False)
value = tf.keras.layers.Dense(head_size,input_shape=(32,), activation=None,use_bias=False)
k = key(x) # (B, T, 16)
q = query(x) # (B, T, 16)
wei = tf.matmul(q,tf.transpose(k,perm=[0,2,1]))
wei = tf.linalg.band_part(wei, -1, 0)
wei = tf.where(
tf.equal(wei,tf.constant(0, dtype=tf.float32)),
-np.inf,
wei)
wei = tf.nn.softmax(wei,-1)
print(wei)
v = value(x)
out = tf.matmul(wei, v)
print(out.shape)Single-head self-attention
After the code shown in the previous section is understood we can integrate it with the main body like this. But from this point onwards I feel the shapes or matrices could have introduced a bug or two even though the code executed without errors. Further investigation is needed. Primarily the mechanism used to port the original Pytorch to TensorFlow is somewhat arduous.
Here I have shown only the relevant changes. I changed block_size to 32 and I also noticed I could generate only upto 32 characters after training.
head_size = 16
dropout = 0.0
n_embd = 32
block_size = 32
class BigramModel(tf.keras.Model):
def __init__(self,vocab_size):
super().__init__()
self.token_embedding_table = Embedding(vocab_size,n_embd)
self.position_embedding_table = Embedding(block_size, n_embd)
self.sa_head = Head(n_embd)
self.lm_head = tf.keras.layers.Dense(vocab_size, input_shape=(n_embd,), activation=None, use_bias=False)
def call(self,idx,targets=None):
# print(f'idx in call is {idx} and shape is {tf.shape(idx)}')
B = 1
if tf.size(tf.shape(idx)) == 1:
T = tf.shape(idx)
else:
T = tf.shape(idx)[1]
tok_emb = self.token_embedding_table(idx)
pos_emb = self.position_embedding_table(tf.range(T))
x = tf.add(tok_emb, tf.expand_dims(pos_emb,axis=0)) # (B,T,C)
# print(f'Shape of tf.add(tok_emb, pos_emb) is {tf.shape(x)}')
x = self.sa_head(x) # (B,T,C)
logits = self.lm_head(x) # (B,T,vocab_size)
if targets is None:
loss = None
else:
bce = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
# loss = bce(targets,tf.squeeze(logits)).numpy()
loss = bce(targets, tf.squeeze(logits))
return logits, loss
def generate(self,idx,max_new_tokens):
i = tf.constant(0)
c = lambda i, d: tf.less(i, max_new_tokens)
def b(i, idx):
# print(idx)
logits,loss = self(idx)
# print(f'Shape of logits is {tf.shape(logits)}')
logits = logits[:,-1,:]
probs = tf.nn.softmax(logits)
# print(f'Shape of probs is {tf.shape(probs)}')
idx_next = tfp.distributions.Multinomial(total_count=1,probs=probs)
idx = tf.concat([idx,
tf.reshape(tf.squeeze(
tf.cast(tf.where(
tf.reshape(idx_next.sample(1),(vocab_size))),tf.int64))
,(1,))],0)
return tf.add(i, 1), idx
_, idx = tf.while_loop(c, b, loop_vars=[i, idx])
# print(f'idx in generate is {idx}')
return idx
class Head(tf.keras.Model):
def __init__(self, head_size):
super().__init__()
self.key = tf.keras.layers.Dense(head_size, input_shape=(n_embd,), activation=None, use_bias=False)
self.query = tf.keras.layers.Dense(head_size, input_shape=(n_embd,), activation=None, use_bias=False)
self.value = tf.keras.layers.Dense(head_size, input_shape=(n_embd,), activation=None, use_bias=False)
self.dropout = tf.keras.layers.Dropout(dropout)
def call(self, x):
B = 1
T = 8
C = 32
k = self.key(x) # (B, T, 16)
q = self.query(x) # (B, T, 16)
transpose = tf.transpose(k,perm=[0,2,1])
matmul = tf.matmul(q,transpose)
wei = tf.divide(matmul, 1/tf.sqrt(tf.cast(C,tf.float32)))
tril = tf.linalg.band_part(wei, -1, 0)
tril = tf.where(
tf.equal(tril,tf.constant(0, dtype=tf.float32)),
-np.inf,
tril)
wei = tf.nn.softmax(tril,-1)
# print(wei)
v = self.value(x)
out = tf.matmul(wei, v)
# print(f'Shape of wei is {tf.shape(out)}')
return outEven though there is no error and the loss goes down there is something missing here.
Start of epoch 0
Training loss at step 0: 4.3814
Seen so far: 1 samples
Training loss at step 200: 3.0663
Seen so far: 201 samples
Training loss at step 400: 3.7423
Seen so far: 401 samples
Training loss at step 600: 3.2426
Seen so far: 601 samples
Training loss at step 800: 3.7633
Seen so far: 801 samples
Training loss at step 1000: 3.2032
Seen so far: 1001 samples
Training loss at step 1200: 3.3238
Seen so far: 1201 samples
Training loss at step 1400: 2.9144
Seen so far: 1401 samples
Training loss at step 1600: 2.8216
Seen so far: 1601 samples
Training loss at step 1800: 2.8043
Seen so far: 1801 samples
Training loss at step 2000: 2.9060
Seen so far: 2001 samples
Training loss at step 2200: 2.8439
Seen so far: 2201 samples
Training loss at step 2400: 2.6887
Seen so far: 2401 samples
Training loss at step 2600: 3.2501
Seen so far: 2601 samples
Training loss at step 2800: 2.8547
Seen so far: 2801 samples
Training loss at step 3000: 2.5416
Seen so far: 3001 samples
Training loss at step 3200: 3.0969
Seen so far: 3201 samples
Training loss at step 3400: 2.8165
Seen so far: 3401 samples
Training loss at step 3600: 2.6081
Seen so far: 3601 samples
Training loss at step 3800: 3.3640
Seen so far: 3801 samples
Training loss at step 4000: 2.5854
Seen so far: 4001 samples
Training loss at step 4200: 2.6794
Seen so far: 4201 samples
Training loss at step 4400: 2.5642
Seen so far: 4401 samples
Training loss at step 4600: 3.0458
Seen so far: 4601 samples
Training loss at step 4800: 2.7516
Seen so far: 4801 samples
Training loss at step 5000: 2.6254
Seen so far: 5001 samples
Training loss at step 5200: 2.6835
Seen so far: 5201 samples
Training loss at step 5400: 2.8002
Seen so far: 5401 samples
Training loss at step 5600: 2.8748
Seen so far: 5601 samples
Training loss at step 5800: 2.8769
Seen so far: 5801 samples
Training loss at step 6000: 3.0199
Seen so far: 6001 samples
Training loss at step 6200: 3.1819
Seen so far: 6201 samples
Training loss at step 6400: 2.8952
Seen so far: 6401 samples
Training loss at step 6600: 2.7828
Seen so far: 6601 samples
Training loss at step 6800: 2.9310
Seen so far: 6801 samples
Training loss at step 7000: 3.0834
Seen so far: 7001 samples
Training loss at step 7200: 2.9211
Seen so far: 7201 samples
Training loss at step 7400: 2.7214
Seen so far: 7401 samples
Training loss at step 7600: 2.9595
Seen so far: 7601 samples
Training loss at step 7800: 3.1095
Seen so far: 7801 samples
Training loss at step 8000: 2.7729
Seen so far: 8001 samples
Training loss at step 8200: 2.6387
Seen so far: 8201 samples
Training loss at step 8400: 3.0497
Seen so far: 8401 samples
Training loss at step 8600: 2.9283
Seen so far: 8601 samples
Training loss at step 8800: 2.7154
Seen so far: 8801 samples
Training loss at step 9000: 2.8881
Seen so far: 9001 samples
Training loss at step 9200: 2.8348
Seen so far: 9201 samples
Training loss at step 9400: 2.8528
Seen so far: 9401 samples
Training loss at step 9600: 2.5401
Seen so far: 9601 samples
Training loss at step 9800: 3.1643
Seen so far: 9801 samples
['1', 'G', "'", 'n', 't', 'c', 'o', 'm', 'e', ',', 'I', 'f', 'A', 'n', 'd', 't', 'h', 'i', 'm', "'", 's', 'w', 'o', 't', 'h', 'i', 's', 'i', 'n', 'g', 'a', 't']Debugging
block_size value is the context that we want to keep track of. But if we want to generate more than the block_size,
pos_emb = self.position_embedding_table(tf.range(T))does not have that in its scope. So I clip the stream of characters like this. This fixes the problem.
idx_cond = idx[-block_size:]
logits,loss = self(idx_cond)Last 2 can be selected like this example shows.

Multi-head attention
At this stage I find that the TensorFlow code looks almost similar to the original Pytorch code and it is easier to reason about. It also works without posing significant dificulties.
The change to the BigramModel is just one line when we introduce multiple heads of attention. A diagram or two will make this clear.
class BigramModel(tf.keras.Model):
def __init__(self,vocab_size):
super().__init__()
self.token_embedding_table = Embedding(vocab_size,n_embd)
self.position_embedding_table = Embedding(block_size, n_embd)
self.sa_head = MultiHeadAttention(n_head, head_size) #Head(n_embd)
self.lm_head = tf.keras.layers.Dense(vocab_size, input_shape=(n_embd,), activation=None, use_bias=False)The class that implements it is this. n_head is set to 4. I use my laptop’s CPU and till this stage it works. But if I tune these hyperparameters and make the network deeper I will need a GPU.
class MultiHeadAttention(tf.keras.Model):
""" multiple heads of self-attention in parallel """
def __init__(self, num_heads, head_size):
super().__init__()
self.heads = [Head(head_size) for _ in range(num_heads)]
self.proj = tf.keras.layers.Dense(n_embd, input_shape=(n_embd,), activation=None, use_bias=False)
self.dropout = tf.keras.layers.Dropout(dropout)
def call(self, x):
out = tf.concat([h(x) for h in self.heads],-1)
out = self.dropout(self.proj(out))
return outI also changed the dataset(https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt) and it seamlessly worked after that.
input = tf.io.read_file("/Users/anu/PycharmProjects/TensorFlow2/input.txt")
length = int(tf.strings.length(input))The code prints properly now.
_, generation = decode(m.generate(tf.zeros((1,),tf.int64),300))
array = np.array(["".join(i) for i in generation.numpy()[:].astype(str)])
s = ''.join(array)
print(s)The output is this. It is still not trained sufficiently but the loss goes down further than before.
FERENIO: Phath athill bof: aser EA E: Mureadest whhere De Ave Po. YiH,Ud Pre SO S: Dos Ton Kosed I I I Hond I LO EcVAwe RURE: I H Kun Id Rhatlt I. Pal Gasnt I, VU HE VISNE
KRING E ITIRIRCGOBEUUSESIMSIOFURI: Lop E: Arse, LOLOS: Khas Ame I I RI: SO Ar-Bu’teo Ofshup Otm 3 Sunscand Reten, Cutxy Tou fl
Further architectural changes
I followed the original Pytorch code closely and this is the final piece of the puzzle. A few changes are introduced to fine-tune the networks. But we have to remember that I am training this using a GPU. So the loss is lower than before now but the text is still gibberish.
Changes to the BigramModel
class BigramModel(tf.keras.Model):
def __init__(self,vocab_size):
super().__init__()
self.token_embedding_table = Embedding(vocab_size,n_embd)
self.position_embedding_table = Embedding(block_size, n_embd)
# self.sa_head = MultiHeadAttention(n_head, head_size) #Head(n_embd)
self.blocks = Block(n_embd, n_head=n_head)
self.ln_f = tf.keras.layers.LayerNormalization() # final layer norm
self.lm_head = tf.keras.layers.Dense(vocab_size, input_shape=(n_embd,), activation=None, use_bias=False)
def call(self,idx,targets=None):
# print(f'idx in call is {idx} and shape is {tf.shape(idx)}')
B = 1
if tf.size(tf.shape(idx)) == 1:
T = tf.shape(idx)
else:
T = tf.shape(idx)[1]
tok_emb = self.token_embedding_table(idx)
pos_emb = self.position_embedding_table(tf.range(T))
x = tf.add(tok_emb, tf.expand_dims(pos_emb,axis=0)) # (B,T,C)
# print(f'Shape of tf.add(tok_emb, pos_emb) is {tf.shape(x)}')
x = self.blocks(x) # (B,T,C)
x = self.ln_f(x) # (B,T,C)
logits = self.lm_head(x) # (B,T,vocab_size)New Model classes
class FeedFoward(tf.keras.Model):
""" a simple linear layer followed by a non-linearity """
def __init__(self, n_embd):
super().__init__()
self.net = tf.keras.Sequential(
layers=[
tf.keras.layers.Dense(4 * n_embd, input_shape=(None,n_embd), activation=None, use_bias=False),
tf.keras.layers.ReLU(),
tf.keras.layers.Dense(n_embd, input_shape=(4 * n_embd,), activation=None, use_bias=False),
tf.keras.layers.Dropout(dropout)
]
)
def call(self, x):
return self.net(x)
class Block(tf.keras.Model):
""" Transformer block: communication followed by computation """
def __init__(self, n_embd, n_head):
# n_embd: embedding dimension, n_head: the number of heads we'd like
super().__init__()
head_size = n_embd // n_head
self.sa = MultiHeadAttention(n_head, head_size)
self.ffwd = FeedFoward(n_embd)
self.ln1 = tf.keras.layers.LayerNormalization()
self.ln2 = tf.keras.layers.LayerNormalization()
def call(self, x):
x = tf.add(x , self.sa(self.ln1(x)))
x = tf.add(x , self.ffwd(self.ln2(x)))
return xConclusion
This exercise helped me understand most of the Transformer architecture. But I coudln’t code this myself after reading research papers directly. I have to watch some videos or port code to TensorFlow. I can only work with an existing knowledge base. I will push the code to Git and look at other architectures as the field is advancing rapidly.
