Tikz Notes

Latex code that I use to draw various types of diagrams.
[auto, node distance=5cm]
\tikzstyle{block} = [draw, rectangle, minimum height=3em, minimum width=3em]
\tikzstyle{virtual} = [coordinate]
% Place nodes
\node [virtual] (input) {};
\node [virtual] (input1) {};
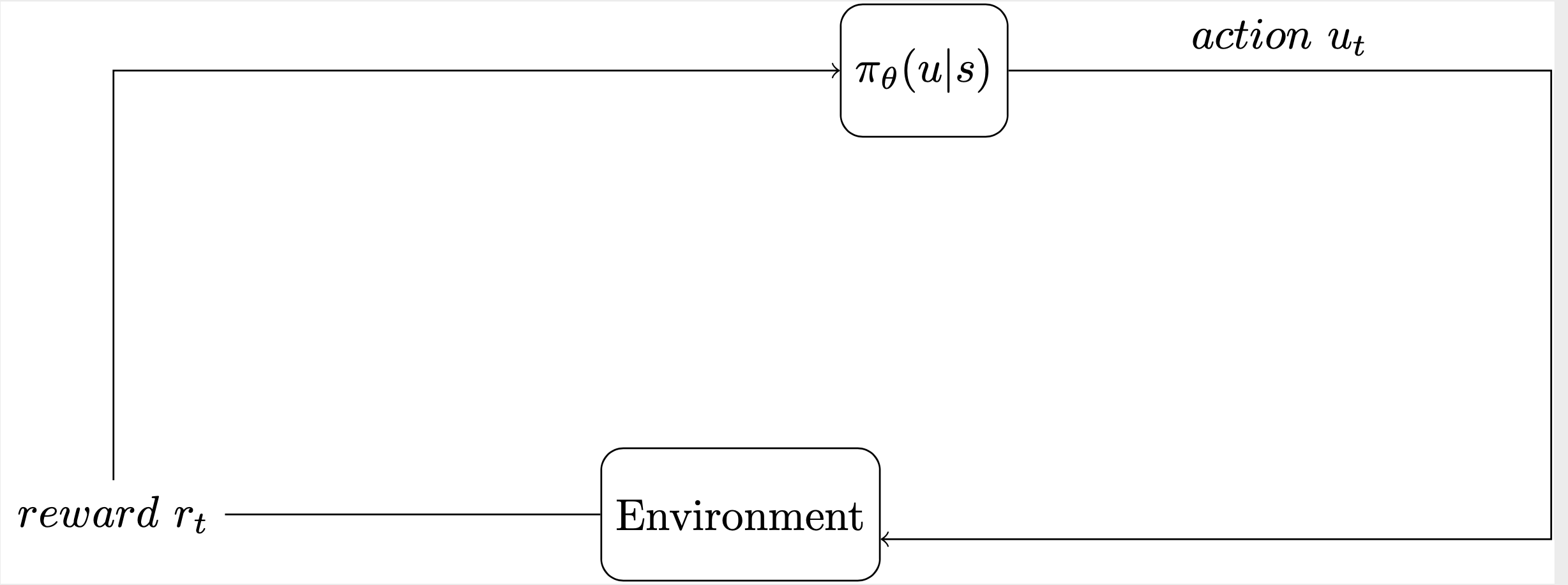
\node [rounded corners=5pt][name=t,block, right of=input] (model) {\(
\pi_\theta (u | s )
\)};
\node [virtual, right of=model] (output) {};
\node [virtual, right of=model] (feedback) {};
\node [rounded corners=5pt][name=e,block, below right of=input1] (model1) {Environment};
\node [virtual, above left of=model1] (reward) {};
\node [name=i,virtual, below left] (input1) {};
\node [name=r, left of=model1] {\( reward \ r_t \)} (reward);
% Connect nodes
\draw [-] (model) -- node [name=y]
{\(action \
u_t \)}
(output);
\draw [->] (y) |- (feedback) |- (model1.-10);
\draw [->] (model1.180) |- (r) |- (model.-180);
\Large
\tikzstyle{block} = [draw=none,,rounded corners=2.9mm,minimum width=4.2mm,minimum height=3.7mm, draw=violet!80,thick, text width=.9cm,,font=\bfseries, align=center, fill=cyan!14]
%nodes
\node[block, anchor=north] (q) {\color{black}{\boldmath$Q_{1}$}};
\node[block, above=40mm of q] (k) {\color{black}{\boldmath$K_{1}$}};
\node at ($(q.north)-(2,-2)$) [block] (x1) {\color{black}{\boldmath$x_{1}$}};
\node[block, right=2cm of x1.center, anchor=center] (v) {\color{black}{\boldmath$V_{1}$}};
%lines
\draw[{Stealth[scale=1.3,angle'=45,open]}-,semithick][rounded corners=2] (q) -- node[midway, label=above:{{\boldmath$W^{q}$}}] {}($(q)-(1,0)$) |- ($(x1.east)+(0,.1)$);
\draw [{Stealth[scale=1.3,angle'=45,open]}-,semithick][rounded corners=2] (k) -- node[midway, label=above:{{\boldmath$W^{k}$}}] {}($(k)-(1,0)$) |- ($(x1.east)+(0,.1)$);
\draw [{Stealth[scale=1.3,angle'=45,open]}-,semithick][rounded corners=2] (v) -- node[midway, label=above:{{\boldmath$W^{v}$}}] {}($(v)-(1,0)$) |- ($(x1.east)+(0,.1)$);
%nodes
\node[-{Latex[black,length=5mm,width=2mm]},semithick][block, below=54mm of k] (k1) {{\boldmath$K_{2}$}};
\node[block, anchor=north, below=43mm of k1] (q1) {\color{black}{\boldmath$Q_{2}$}};
\node at ($(q1.north)-(2,-2)$) [block , below=57mm of x1] (x2) {\color{black}{\boldmath$x_{2}$}};
\node[block, right=2cm of x2.center, anchor=center] (v1) {\color{black}{\boldmath$V_{2}$}};
%lines
\draw[{Stealth[scale=1.3,angle'=45,open]}-,semithick][rounded corners=2pt] (q1) -- node[midway, label=:{{\boldmath$W^{q}$}}] {}($(q1)-(1,0)$) |- ($(x2.east)+(0,.1)$);
\draw [{Stealth[scale=1.3,angle'=45,open]}-,semithick][rounded corners=2] (k1) -- node[midway, label=left:{{\boldmath$W^{k}$}}] {}($(k1)-(1,0)$) |- ($(x2.east)+(0,.1)$);
\draw [{Stealth[scale=1.3,angle'=45,open]}-,semithick][rounded corners=2] (v1) -- node[midway, label=above:{{\boldmath$W^{v}$}}] {}($(v1)-(1,0)$) |- ($(x2.east)+(0,.1)$);
%nodes
\node[block, below=57mm of k1] (k2) {\color{black}{\boldmath$K_{T}$}};
\node[block, anchor=north, below=40mm of k2] (q2) {\color{black}{\boldmath$Q_{T}$}};
\node at ($(q2.north)-(2,-2)$) [block , below=57mm of x2] (x3) {\color{black}{\boldmath$x_{T}$}};
\node[block, right=2cm of x3.center, anchor=center] (v2) {\color{black}{\boldmath$V_{T}$}};
%lines
\draw [{Stealth[scale=1.3,angle'=45,open]}-,semithick][ rounded corners=2] (q2) -- node[midway, label=above:{{\boldmath$W^{q}$}}] {}($(q2)-(1,0)$) |- ($(x3.east)+(0,.1)$);
\draw [{Stealth[scale=1.3,angle'=45,open]}-,semithick][rounded corners=2] (k2) -- node[midway, label=left:{{\boldmath$W^{k}$}}] {}($(k2)-(1,0)$) |- ($(x3.east)+(0,.1)$);
\draw [{Stealth[scale=1.3,angle'=45,open]}-,semithick][rounded corners=2] (v2) -- node[midway, label=above:{{\boldmath$W^{v}$}}] {}($(v2)-(1,0)$) |- ($(x3.east)+(0,.1)$);
\node (r1) [draw=none,rounded corners=.5cm,line width=.6mm, below=1mm of q, draw=violet!80, minimum width=5.2cm,minimum height=6.7cm]{};
\node (r2) [draw=none,rounded corners=.5cm,line width=.6mm, right=33mm of v, draw=blue!80, minimum width=3.5cm,minimum height=1.6cm]{};
\node (r3) [draw=none,rounded corners=.5cm,line width=.5mm, below=37mm of r2, draw=blue!80, minimum width=3.5cm,minimum height=1.6cm]{};
\node (r4) [draw=none,rounded corners=.5cm,line width=.5mm, below=56mm of r3, draw=blue!80, minimum width=3.5cm,minimum height=1.4cm]{};
\node [block , right=37mm of v] (q21) {\color{black}{\boldmath$Q_{2}$}};;
\node [block , right=3mm of q21] (k11) {\color{black}{\boldmath$K_{1}$}};;
\node [below=of r2.north] {\color{black}{\boldmath$T$}};;
\node [below= of r3.north] {\color{black}{\boldmath$T$}};;
\node [below= of r4.north] {\color{black}{\boldmath$T$}};;
\node [block , fill=YellowGreen!40,above=37mm of q21] (a21) at ([yshift=-2cm]$(q21)!0.5!(k11)$) {\color{black}{\boldmath$a_{2,1}$}};;
\node [block , below=45mm of q21] (q22) {\color{black}{\boldmath$Q_{2}$}};;
\node [block , right=3mm of q22] (k12) {\color{black}{\boldmath$K_{2}$}};;
\node [block , fill=YellowGreen!40, above=30mm of q22] (a22) at ([yshift=-2cm]$(q22)!0.5!(k12)$) {\color{black}{\boldmath$a_{2,2}$}};;
\node [block , below=64mm of q22] (q23) {\color{black}{\boldmath$Q_{T}$}};;
\node [block , right=3mm of q23] (k13) {\color{black}{\boldmath$K_{T}$}};;
\node [block , fill=YellowGreen!40,above=34mm of q23] (a23) at ([yshift=-2cm]$(q23)!0.5!(k13)$) {\color{black}{\boldmath$a_{2,3}$}};;
\draw [color=Orange,line width=1.95pt,dotted][rounded corners=2] (v) -- (5.2,0);
\node [block , fill=Violet!20,right=83mm of v1] (A2) {\color{black}{\boldmath$A_{2}$}};
\draw [-{Stealth[scale=1.3,angle'=45,open]},color=Orange,line width=1.95pt,dotted][rounded corners=2](5.2,0) -- ($(A2)-(0.7,0)$);
\draw [-{Stealth[scale=1.3,angle'=45,open]},line width=1.95pt,color=Orange,dotted][rounded corners=2](5.2,-8) -- ($(A2)-(0.7,0)$);
\draw [line width=1.95pt,color=Orange,dotted][rounded corners=2] (v2) -- (5.2,-8);
\draw [-{Stealth[scale=1.3,angle'=45,open]},line width=1.95pt,color=Orange,dotted][rounded corners=2] (v1) -- ($(A2)-(0.8,0)$);
\draw [line width=1.95pt,color=Orange,dotted][rounded corners=2] ($(r2.south)-(1,0)$) -- (5.2,0);
\draw [line width=1.95pt,color=Orange,dotted][rounded corners=2] ($(r4.north)-(1.3,.1)$) -- (5.2,-8);
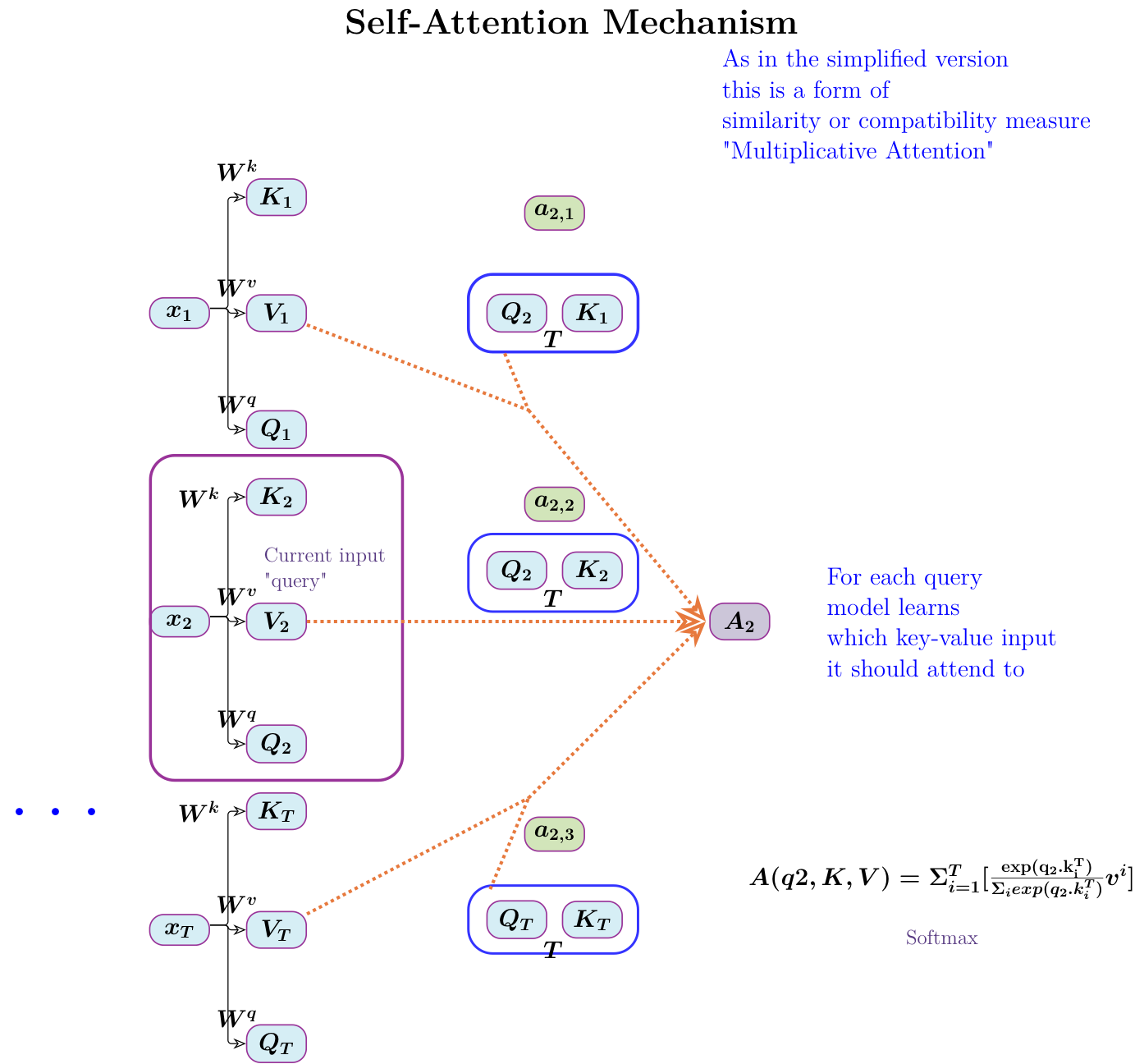
\node[text=blue,align=left] at (13,6) {As in the simplified version\\ this is a form of \\ similarity or compatibility measure \\ "Multiplicative Attention" \\};
\node [text=blue,align=left,right=of A2] (text1) {For each query\\ model learns\\ which key-value input \\ it should attend to};
\node [ below=34mm of text1] (formula1) {\color{black}{\boldmath$A(q2,K,V)=\Sigma_{i=1}^T[\frac{\mathrm{exp(q_2 . k_i^T)}}{\Sigma_iexp(q_2 . k_i^T)} v^i]
$}};
\node[text=RoyalPurple,below=3mm of formula1,align=left,font=\fontsize{12pt}{15pt}\selectfont] (sm) {Softmax\\};
\node[text=RoyalPurple,align=left,font=\fontsize{12pt}{15pt}\selectfont] at (1,-3.5) {Current input\\ "query"\\};
\node at ($(k2)!.5!(q2)$) [text=blue,left=25mm of k2,font=\fontsize{52pt}{35pt}\selectfont]{\ldots};
\node[above,font=\huge\bfseries] at (current bounding box.north) {Self-Attention Mechanism};
[fill=blue!35,fill opacity=.5445]
\matrix[left delimiter=(,right delimiter=)] (magic) [matrix of nodes]
{
0 & 1 & 2 & 3 & 4\\
0 & 0 & 5 & 6 & 7\\
0 & 0 & 0 & 8 & 9\\
0 & 0 & 0 & 0 & 10\\
0 & 0 & 0 & 0 & 0\\
};
\fill
(magic-1-1.north west) |- (magic-5-5.north east) |-
(magic-5-1.south west) |- (magic-5-5.east) |-
(magic-5-5.south) |- (magic-5-5.east)|-
(magic-5-1.north west) |- (magic-5-5.west)|-
(magic-5-2.north west) |- (magic-5-5.west)|-
(magic-5-3.north west) |- (magic-5-5.west)|-
(magic-5-4.north west) |- (magic-5-5.west)|-
(magic-5-5.north west) |- (magic-5-5.east);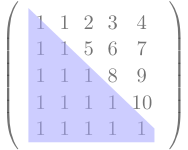
Written on February 17, 2023
